(几何光学)费马原理,你真的明白了吗？

一、费马原理的表述

费马原理物理表述：

费马原理是这么说的：过空间中两定点的光，实际路径总是光程平稳值的路径。

费马原理数学表述：

路径积分

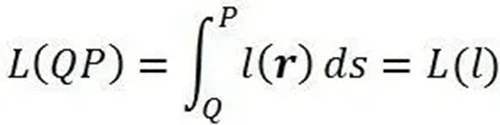
是路径l(r)的函数，这在数学上被称为泛函。泛函的平稳值要求其“一阶变分为零”，即

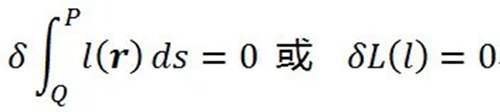
它是变分方程，目的是求出平稳值路径。费马原理的数学表达式就是它。这里的是δ变分算符。

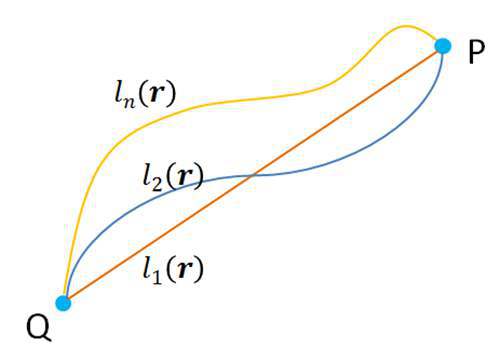
二、什么是路径积分、泛函、变分路径积分假设光线从Q点出发，到达P点，有n条路径；每一条路径都有对应的函数表示。每条路有多长呢？这时候就用路径积分来计算（下图只画了三条，其他未画出）

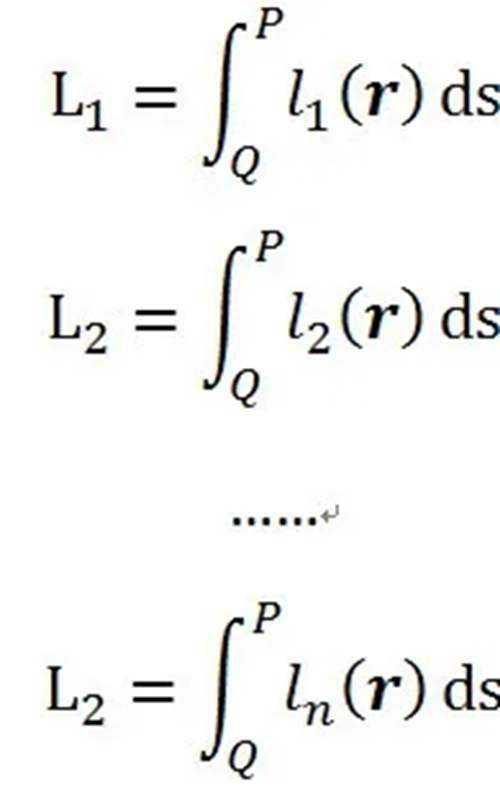
泛函

路径积分在计算每一条路径长度时，每条路径积分函数都对应一个数值（路径长度）：

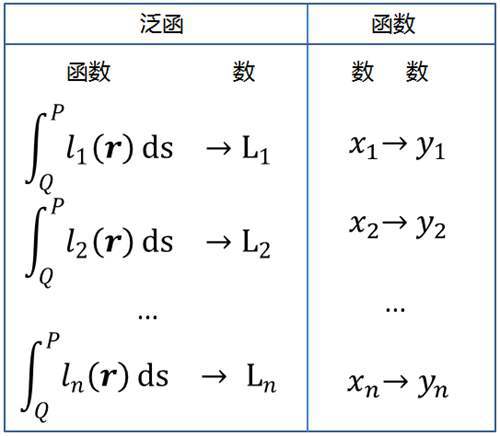
这类似于数学定义函数说的变量y和自变量x的一一对应关系；泛函就是：“变量”数值和“自变量”函数的一一对应关系。简单说下，泛函是将函数空间（无限维空间）映射到数域。

变分

理解了泛函，那么变分就很简单了，对泛函求微分，我们用新的名词叫做变分。

三、平稳值中的极大值、极小值、常数不矛盾吗？

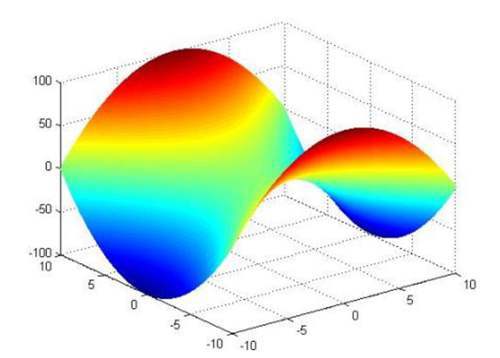
其实当我们把泛函（整个函数空间）全部表示在图像中的时候，得到的图像类似于马鞍图（见下图）

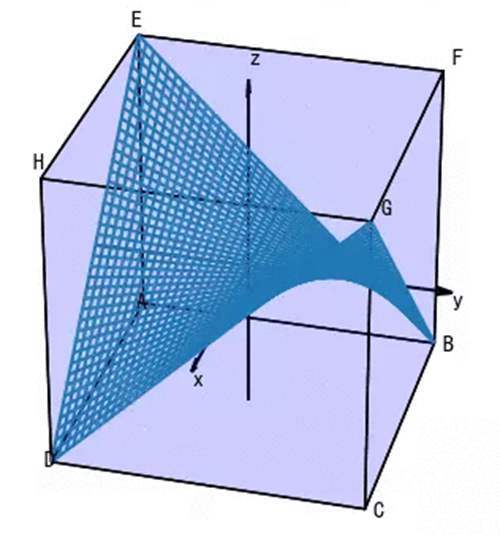
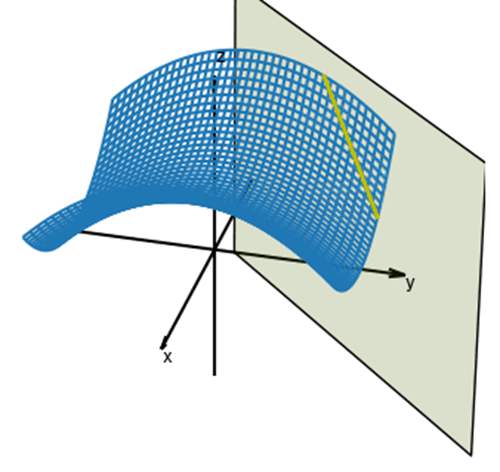
当光线在某介质中传播时，该介质以及边界条件的限制，导致泛函只能显示出一部分；（平面可以看成限制条件，平面与马鞍面相交的黄线可以认为是光线在某介质中传播时泛函）

极大值（黄线对应的泛函求变分等于零可得极大值）

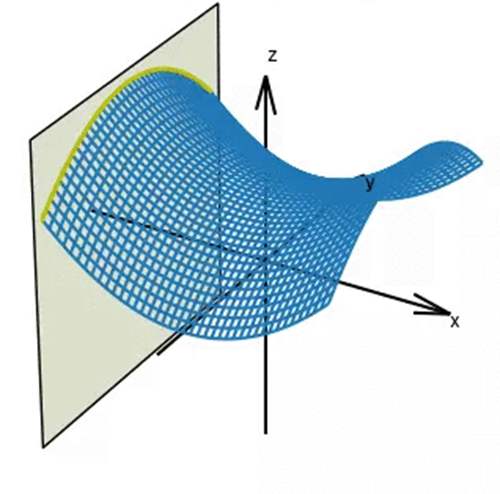
极小值（黄线对应的泛函求变分等于零可得极小值）

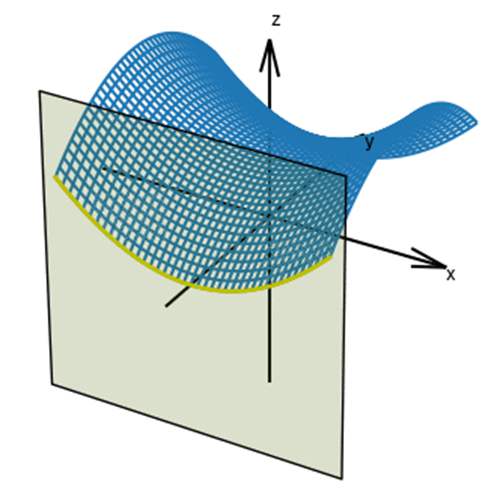
常数（黄线对应的泛函求变分等于零可得常数）

四、能找出具体的例子吗？

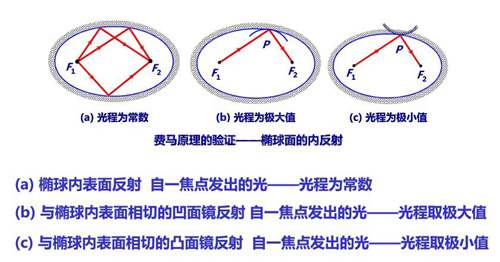
此时不得不请出我们最特殊的光学器件——椭球镜；我们知道椭圆上任意一点到两个焦点距离之和都相等。

以上就是（(几何光学)费马原理,你真的明白了吗？）全部内容，收藏起来下次访问不迷路！