基本计算 求极限
基本计算 求极限
连续性
定义是判断极限最基础的东西;
但函数的连续性是计算极限最基础的东西。
有了连续性性质,你就摆脱了必须用定义和玄而又玄的感觉来求极限的现状;
有了连续性性质,你就踏入了能够加减乘除动笔计算的殿堂,一身轻松个屁
首先给出连续性的定义:
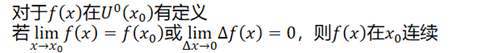
简简单单,平平常常,连续性这么重要,然并卵

当给出以上两个定理后,极限的计算就变得理所当然了,比如:
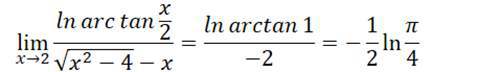
例
代值计算么,谁不会呢
对于复合函数来说,一个重要函数就是幂指函数,求幂指函数的极限:
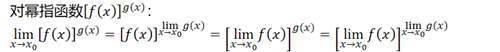
最后都可以直接代值计算了,很棒(雾)
四则运算法则
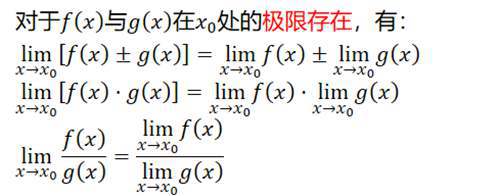
极限存在极限存在极限存在
很多运算都要往加减乘除上靠,那么极限的四则运算如上,能够使用四则运算最重要的条件一定是极限存在
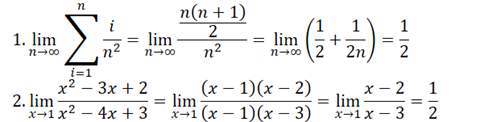
栗子
其实不举例子也罢,很快的,你对它就很亲切了
特殊极限

两种特殊极限,一种运用在三角中,一种是自然常数e的定义
简单地套公式就好
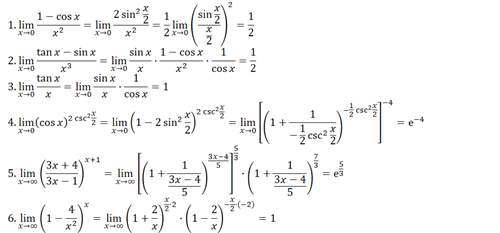
例
特殊极限相对来说可能用得比较少,这种明显能看出来让你用特殊极限的题还是很简单的
等价无穷小量替换
上面说的相对在这可以显露一二,运用等价无穷小量灰常多,人造难度题就喜欢用等价无穷小量换来换去偷袭我们这些挂在高树上的人
关于等价无穷小量以及一些常用的等价无穷小量分出一期,以上
给出定理:

注意重点是相乘除
于是,我们就可以开心地换来换去啦
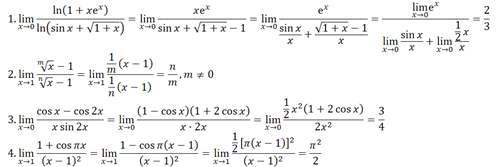
例
但是该等价无穷小量替换的局限性就是对只能在自变量趋于0时的替换,自变量趋于其他值时理论上也可以用等价无穷小量替换,可以自己寻找去证明,可以运用换元的思想转化为自变量趋于0,不过那时候也不一定需要用等价无穷小量替换了
洛必达LHospital法则
来了,我高中最喜欢的洛必达
给出法则:

LHospital法则
高中选填用得最舒服,理论也很简单,证明看书,使用Cauchy中值定理
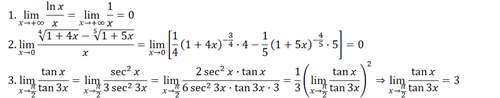
例
例中3完全可以换元用等价无穷小量替换,还特别简单,这么做只是为了试验LHospital法则,不要在意这些细节……
泰勒Taylor展开
一般泰勒展开求极限是万不得已的最终措施,太复杂,慎用
求极限中的泰勒展开只用到带皮亚诺Peano余项的Taylor公式及Maclaurin公式:
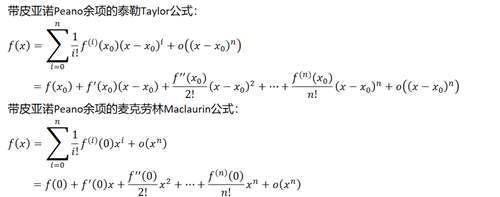
再常用一点,就是这些常用的带皮亚诺余项的麦克劳林公式:
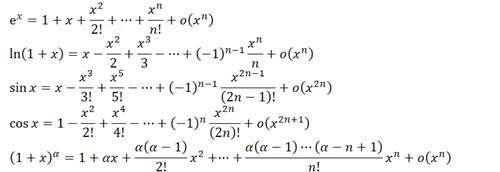
求极限中运用泰勒展开还有亿点点细节:
关于极限中无穷小量的运算:
对无穷小量求极限等于0是真理,不多说
将自变量与无穷小量相乘,乘进去(应该算变成更高阶了)
而极限中无穷小量相加减的运算:

更高阶的无穷小量因为在计算中趋于0,所以可以略去,在展开过程中也可确定展开的阶数
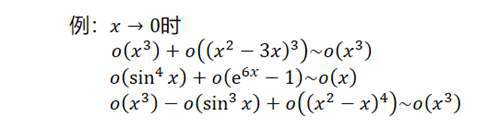
例
关于极限中Taylor展开的阶数问题:
Taylor展开有n阶项,我们不可能全部展开,而只要展开到一定的阶数极限就能够算出来,一般判断展开的阶数是根据分子分母的相关性而来,展开到阶数相当就好,在刷题练习中熟能生巧

例
泰勒展开还是不太常用,像例中4、5这种用洛必达很烦就用泰勒展开,用着开心就好
技巧
“终极秘籍”“决胜之手”
有没有觉得自己空有极限的一切概念却对求极限依然束手无策、无从下手
有没有觉得自己掌握了求极限的一切方法却依然算不出来一些题目
(比如说我)
公式是死的,题目是活的,思维也是活的,所以各种变换应该信手拈来(×)
换元:
倒代换,常用于无穷小量与无穷大量的转换,比较常见:
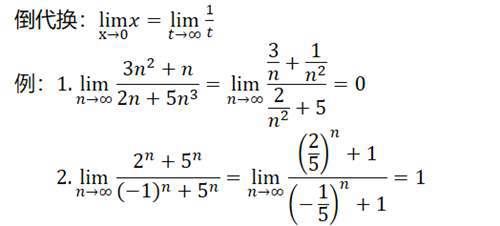
还有幂代换、三角代换,虽然不在求极限中常用,但在求积分中……(以后再说)
还有其他类型的换元,就是普遍换元,比如说:
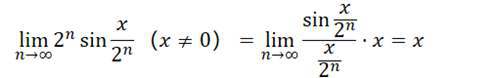
取指对数:
通常对幂指函数进行指对数代换:
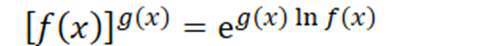
用得太多了,哪怕是第二种特殊极限也可以用取指对数来算,尤其对于一些人造难度题……
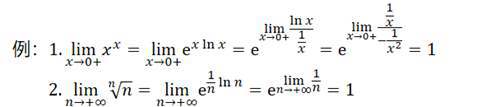
有理化:
对含根式的式子进行有利的变换,包括分母有理化和分子有理化(还有多式同时有理化,也就是因式分解)
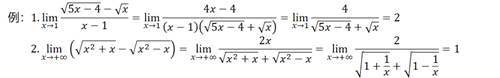
部分分式分解:
将式子裂项然后用四则运算理论上(极限存在)就可以算出来
部分分式分解大多还是用在简单的真分式裂项,比如说:
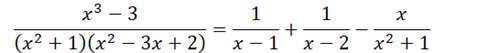
部分分式分解
像之前8个未知数求解的难度不要当真
夹逼定理:
夹逼定理用于求极限一般在三角中、在数列中,大多不会放缩两边(两边放缩的题用其他方法都可以解出来了叭),也就是放一边为0

夹逼定理或许可以称为方法而不是技巧,它在计算方面不多
无穷小量与有界量的积:
利用无穷小量与有界量的积为无穷小量的性质可以解决许多复杂极限,在含三角的极限中常见

无穷小量与有界量的积或许也可以称为方法而不是技巧,但它确实巧妙
平方差
有的时候a,一个一眼看出用平方差公式就能轻松解决的求极限题可能会卡死你乃至心态爆炸……比如说:
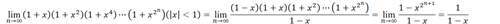
因为一眼看不出(枯了)
结语
刷题
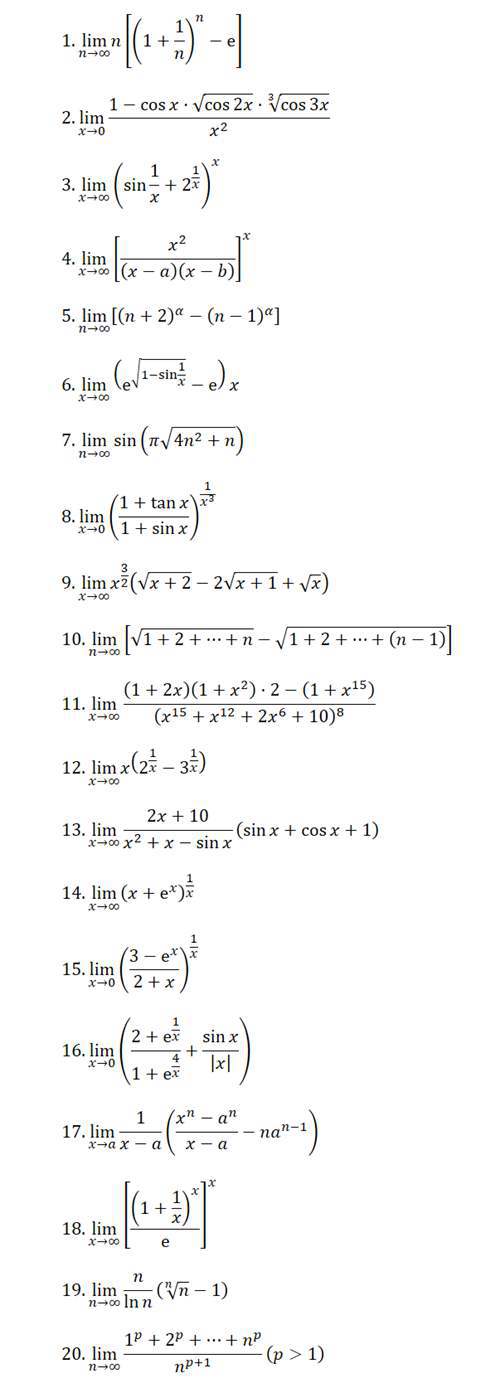
没什么好说的,刷题刷题刷刷题(泪目)
以上方法差不多就够用了叭,变态人造难度题还是算了(指20)
什么?题目不够么?
再来点:

还有与解方程的结合:

还有变上下限积分求极限hhh:
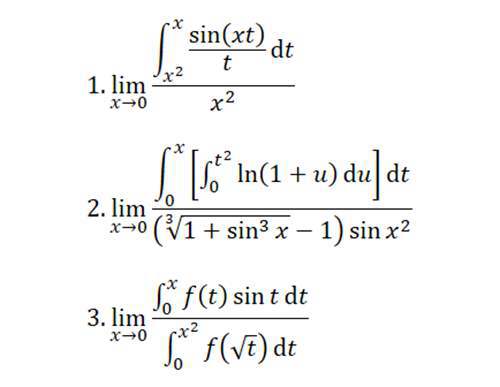
不会吧不会还不够叭,那——
诸君加油
以上就是(基本计算 求极限)全部内容,收藏起来下次访问不迷路!